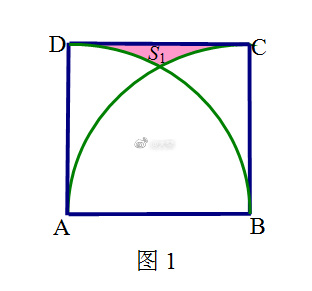
【题目】如图1，在边长为1的正方形ABCD中，求阴影部分的面积

【题目】如图1，在边长为1的正方形ABCD中，求阴影部分的面积 .

【解法一：算术法】

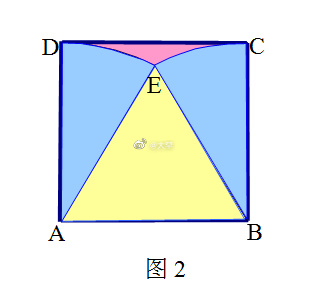
  如图2，设弧AC与弧BD交于点E，则∠CBE=DAE=30°，则
  阴影部分面积=正方形ABCD面积-(2×扇形CBE面积+△ABE面积)
  =16-[2×(1/12)π×4^2+(√3/4)×4^2]
  =16-(8/3)π-4√3.

【解法二：列方程组法】

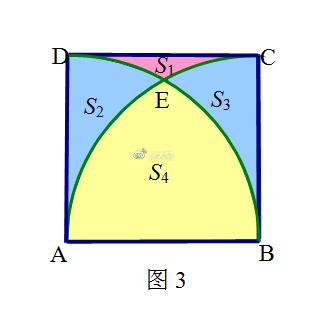
  如图3，把正方形ABCD分成四个部分，分别记为S(1)、S(2)、S(3)、S(4)，则有
  S(1)+2S(2)+S(4)=16①， S(2)+S(4)=4π②， S(4)=(16/3) π-4√3③，
  由②③得：S(2)= 4√3- (4/3) π，
  代入①，有
  S(1)= 16-(8/3)π-4√3.

【说明】

• ⑴小学六年级不能做本题。因为本题回避不了无理数，而无理数在小学六年级是不学的。

• ⑵在小学六年级奥数里可以做此题。不过，事先要补充勾股定理、无理数等知识。初二以上的学生应该会做。

• ⑶此题用不着用定积分来做。那是高射炮打蚊子。不仅如此，还自找麻烦，弄巧成拙。