妙解连体正方形问题（1）

妙解连体正方形问题（1）
大罕

两个正方形有一个公共顶点，称为连体正方形．
　

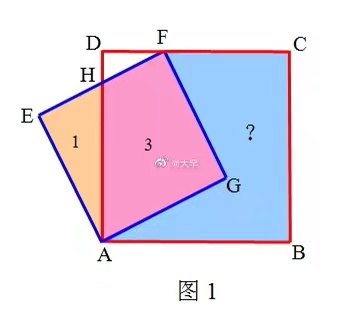
【题目】如图1，连体正方形ABCD和AEFG，橙色和粉色区域的面积为1和3，求蓝色区域的面积．

【解法一：等量公理法】

　　如图2，由正方形AEFG面积＝4，得AE=2，
　　由△AEH面积为1，得EH=1，故AH=√5，
　　作EK⊥AD于K，由AE×EH=AH×EK，得EK=2/√5，
　　∴HK=1/√5，
　　由△EKH ≌△FDH，
　　∴△FDH面积=△EKH面积=1/5，
　　又AD＝AH+HD=√5+1/√5=6/√5，
　　∴正方形ABCD面积为36/5．
　　∴蓝色区域面积＝正方形ABCD面积-△FDH面积-四边形AHFG面积＝36/5-1/5-3=4.
　　

【评论】解法一只需算出△FDH面积即可，是最直接、也是最简单的方法．